Espero que você aprenda muito com este exercício.
Aprofunde-se mais nos seus estudos com : Exercícios Resolvidos
10 exercícios de tabela verdade resolvidos com gabarito para testar seus conhecimentos sobre conectivos lógicos, proposições simples e compostas, e muito mais!
Quer aprender tabelas verdade com esta lista de exercícios resolvidos com gabarito.
#Índice
Alice estava estudando para o concurso público da prefeitura municipal de Itabira/MG e se deparou com uma questão que solicitava a montagem da tabela verdade de ~(pV~q). Para solucionar ela montou o seguinte quadro:
O número de V encontrado na coluna p v ~q multiplicado pelo número de F encontrado na última coluna é:
A
1.
B
6.
C
9.
D
4.
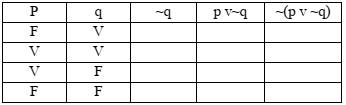
Parte 1 da resolução
- Resolução da negação de q.
-
P q ~q F V F V V F V F V F F V - Resolução da disjunção (Pv~q) cujo símbolo é v e o conectivo é ou.
-
P q ~q (pv~q) F V F F V V F V V F V V F F V V - Resolução da negação da proposição ~(Pv~q).
-
P q ~q (pv~q) ~(pv~q) F V F F V V V F V F V F V V F F F V V F
Resolvida a tabela verdade da proposição ~(pV~q), conforme solicitado no enunciado do exercício sabemos que a coluna de pV~q possui 3 linhas verdadeiras e a coluna ~(pV~q) possui 3 linhas falsas, que multiplicados nos leva a resposta Letra C, 9
Tabela verdade é um dispositivo utilizado no estudo da lógica matemática. A tabela verdade serve para isolar as proposições e seus conectivos em um quadro, facilitando sua compreensão e análise nos mínimos detalhes. Dessa forma, é possível visualizar com mais clareza o que cada parte da sentença quer dizer e extrair seu verdadeiro significado. A tabela verdade busca extrair o sentido verdadeiro de uma sentença lógica.
Considere as proposições p, q, r e S a seguir:
p: Campina Grande é uma cidade.
q: Oscar Niemeyer é um arquiteto brasileiro.
r: O sol gira em torno da terra.
S: p → ~ q ˄ r.
Logo, pode-se afirmar que:
A
Não é possível determinar o valor lógico de S.
B
O valor lógico de S é a verdade.
C
O valor lógico de S é a falsidade.
D
S não tem valor lógico.
E
S é simultaneamente verdadeira e falsa.
Parte 1 da resolução
Para começarmos a resolver este exercício de tabela verdade, o primeiro passo é atribuir valores lógicos(verdadeiro ou falso) para cada proposição lógica simples detectada no enunciado do problema, conforme análise abaixo:
-
Campina Grande é um município brasileiro no estado da Paraíba. Considerada um dos principais polos industriais da Região Nordeste, foi fundada em 1 de dezembro de 1697, tendo sido elevada à categoria de cidade em 11 de outubro de 1864.(Fonte:Wikipedia)
De acordo com o texto acima, podemos considerar que a proposição lógica "Campina Grande é uma cidade." é verdadeira.
-
Oscar Ribeiro de Almeida Niemeyer Soares Filho (Rio de Janeiro, 15 de dezembro de 1907 – Rio de Janeiro, 5 de dezembro de 2012) foi um arquiteto brasileiro, considerado uma das figuras-chave no desenvolvimento da arquitetura moderna. Niemeyer foi mais conhecido pelos projetos de edifícios cívicos para Brasília, uma cidade planejada que se tornou a capital do Brasil em 1960. (Fonte:Wikipedia)
De acordo com o texto acima, podemos considerar que a proposição lógica "Oscar Niemeyer é um arquiteto brasileiro." é verdadeira.
-
A translação da Terra é o movimento que a Terra realiza ao redor do Sol. Uma translação completa ao redor do Sol leva 1 ano sideral ou 365,256363 dias solares. (Fonte:Wikipedia)
De acordo com o texto acima, podemos considerar que a proposição lógica "O sol gira em torno da terra." é falsa.
Parte 2 da resolução
Para chegarmos a resposta dessa questão, letra C(o valor lógico de S é a falsidade), vamos montar uma tabela verdade para a proposição composta S: p → ~ q ˄ r, conforme demonstrado abaixo:
| p | q | r | ~q | p → ~ q | S: p → ~ q ˄ r |
|---|---|---|---|---|---|
| V | V | F | F | F | F |
Observação: Como a proposição lógica p → ~ q ˄ r não tem parênteses, a ordem de resolução é da esquerda para direita.
No estudo das tabela verdades e da lógica proposicional, uma tautologia ocorre quando na última coluna da tabela verdade, todos os valores são verdadeiros independentemente da quantidade de linha da tabela. Já uma contradição é o contrário do que ocorre nos casos de tautologia, ou seja, todos os valores da última coluna de uma tabela verdade são completamente falsos.
Se A e B são proposições simples verdadeiras, então o valor lógico de (A ∧¬B) ⇒¬A é:
A
Falso.
B
Verdadeiro.
C
Tautológico.
D
Impossível de calcular.
E
Impossível de saber.
Parte 1 da resolução
O primeiro passo para resolver esse exercício é montar a tabela verdade simplificada para a proposição(A ∧¬B) ⇒¬A visto que no enunciado do exercício foi dito que tanto A quanto B são proposições simples verdadeiras.
| A | B |
|---|---|
| V | V |
Parte 2 da resolução
Os parênteses da proposição (A ∧¬B) ⇒¬A indica por onde devemos começar a resolução do exercício, ou seja, primeiro vamos resolver a proposição (A ∧¬B), preposição A conjunção de negação da proposição B, conforme demonstrado na tabela verdade abaixo.
| A | B | ¬A | ¬B | A ∧¬B |
|---|---|---|---|---|
| V | V | F | F | F |
Observações:
-
A negação(¬) de uma proposição verdadeira é seu valor inverso, ou seja, se o valor de uma proposição é verdadeiro então sua negação é o valor falso.
-
Já a conjunção(∧) será verdadeira se e somente se ambos os operandos são verdadeiros.
Parte 3 da resolução
Por fim para chegarmos a resposta Letra B verdadeiro, devemos pegar o resultado da proposição (A ∧¬B) e resolver a proposição completa, conforme a tabela verdade abaixo:
| A | B | ¬A | ¬B | A ∧¬B | (A∧¬B)⇒¬A |
|---|---|---|---|---|---|
| V | V | F | F | F | V |
Observações:
-
A condicional(⇒) é falsa se, e somente se, o primeiro operando é verdadeiro e o segundo operando é falso.
-
A alternativa C está errada, pois uma tautologia é uma proposição que sempre será verdadeira independentemente das possíveis valorações das variáveis proposicionais que a compõe. Perceba no exemplo abaixo que se a proposição A sendo verdadeira e proposição B sendo falsa o resultado da proposição (A∧¬B)⇒¬A seria falso, o que indica que não se trata de uma tautologia.
| A | B | ¬A | ¬B | A ∧¬B | (A∧¬B)⇒¬A |
|---|---|---|---|---|---|
| V | F | F | V | V | F |
Uma proposição lógica A será equivalente a uma proposição lógica B se as tabelas-verdade destas duas proposições forem idênticas, mesmo que a proposição A seja diferente de B.
Considere as proposições a, b, c e D a seguir:
a: Luiz Inácio Lula da Silva foi presidente do Brasil.
b: A capital do Rio de Janeiro é São Paulo.
c: A Terra é plana.
D: (a ˄ ~b) ↔ c
Pode-se afirmar que:
A
O valor lógico de D é a falsidade.
B
O valor lógico de D é a verdade.
C
Não é possível determinar o valor lógico de D.
D
D não tem valor lógico.
E
D é simultaneamente verdadeiro e falso.
Parte 1 da resolução
Para começarmos a resolver este exercício de tabela verdade, o primeiro passo é atribuir valores lógicos(verdadeiro ou falso) para cada proposição lógica simples detectada no enunciado do problema, conforme análise abaixo:
-
Luiz Inácio Lula da Silva, nascido Luiz Inácio da Silva mais conhecido como Lula é um político, ex-sindicalista e ex-metalúrgico brasileiro, principal fundador do Partido dos Trabalhadores (PT) e o 35º presidente do Brasil, tendo exercido o cargo de 1º de janeiro de 2003 a 1º de janeiro de 2011. (Fonte:Wikipedia)
De acordo com o texto acima, podemos considerar que a proposição lógica "Luiz Inácio Lula da Silva foi presidente do Brasil." é verdadeira.
-
Rio de Janeiro (frequentemente referida simplesmente como Rio) é um município brasileiro, capital do estado homônimo, situado no Sudeste do país. (Fonte:Wikipedia)
De acordo com o texto acima, podemos considerar que a proposição lógica "A capital do Rio de Janeiro é São Paulo." é falsa.
-
Define-se a forma da Terra como geoide, que tem uma superfície irregular e, portanto, não corresponde a uma esfera. Mais precisamente, o geoide é uma superfície equipotencial do campo da gravidade, ou seja, sobre essa superfície o potencial do campo da gravidade é constante, coincidindo, portanto, com uma superfície de equilíbrio de massas d’água. (Fonte:Atlas Escolar)
De acordo com o texto acima, podemos considerar que a proposição lógica "A Terra é plana." é falsa.
Parte 2 da resolução
Para chegarmos a resposta dessa questão, letra A(o valor lógico de D é a falsidade), vamos montar uma tabela verdade para a proposição composta D: (a ˄ ~b) ↔ c, conforme demonstrado abaixo:
| a | b | c | ~b | a ˄ ~b | (a ˄ ~b) ↔ c |
|---|---|---|---|---|---|
| V | F | F | V | V | F |
Para sabermos a quantidade de linhas que uma tabela verdade terá, basta utilizarmos a fórmula: 'nº de linhas=2^nº de proposições', ou seja, uma tabela verdade com 3 proposições terá 8 linhas, já uma com 4 proposições terá 16 linhas.
Observe a seguinte tabela-verdade em que P e Q são proposições simples:
O espaço “?” é corretamente preenchido com o seguinte valor lógico:
A
Verdadeiro.
B
Incerto.
C
Tautológico.
D
Falso.
E
Impossível de saber.
- Parabéns!
O espaço ‘?’ relacionado com o valor lógico de ‘Q’, é corretamente preenchido com o valor ‘falso’, que nos leva a resposta correta Letra D.
Na tabela verdade dada no enunciado do exercício, a proposição ‘P=>Q’ é uma operação lógica condicional cujo valor é ‘falso’, ou seja, a única possibilidade de uma operação condicional ser ‘falsa’ é a proposição simples ‘P’ possuir o valor lógico ‘verdadeiro’ e a proposição ‘Q’ possuir o valor ‘falso’. Fora a combinação de valores ‘verdadeiro’ e ‘falso’, as demais combinações resultarão no valor lógico ‘verdadeiro’ para quaisquer outras combinações da operação condicional.
| P | Q | P→Q |
|---|---|---|
| V | F | F |
- Errou?
A Letra A está errada, pois se o espaço ‘?’ fosse preenchido com o valor lógico ‘verdadeiro’, então a proposição condicional ‘P=>Q‘ resultaria no valor ‘verdadeiro’, e não ‘falso’ como demonstrado no enunciado da questão.
| P | Q | P→Q |
|---|---|---|
| V | V | V |
A Letra B está errada, pois o valor do espaço ‘?’ não pode ser incerto devido ao fato de termos identificado que ‘P=>Q‘ é uma condicional e também devido ao fato que a descrição do problema ter informado que o valor lógico da proposição simples ‘P’ é ‘’verdadeiro’, ou seja, aplicando um raciocínio lógico inverso, partindo do resultado conseguimos descobrir o valor lógico de ‘Q’.
A Letra C está errada, pois para ser tautológica qualquer que fosse o valor lógico que preenche o espaço ‘?’ correspondente a proposição ‘Q’, o resultado da condicional ‘P=>Q‘ teria que ser ‘verdadeiro’, que não é o caso visto que o próprio enunciado do exercício já informou que o valor lógico da operação ‘P=>Q‘ é ‘falso’.
A Letra E está errada, pois quando a questão informou o valor lógico da condicional ‘P=>Q‘ e também da proposição ‘P’, que por dedução lógica conseguimos saber o valor da proposição ’Q’
Tabelas verdade são muito utilizadas com circuitos lógicos em eletrônica digital, em eletrônica ela possuirá uma coluna para cada valor de entrada e uma coluna final para os valores computados a depender da operação lógica utilizada.
Considere a proposição composta:
Se o jogador reclama ou o técnico protesta, então o juiz não viu a falta e os auxiliares não puderam ajudar.
As quatro proposições simples que a decompõe são:
- P1: o jogador reclama;
- P2: o técnico protesta;
- P3: o juiz não viu a falta;
- P4: os auxiliares não puderam ajudar.
A proposição composta pode, então, ser representada por: P1vP2 → P3vP4.
Assinale a alternativa que lista corretamente os valores assumidos por A e B na última coluna da tabela verdade abaixo.
A
A-V, B-V
B
A-F, B-V
C
A-V, B-F
D
A-F, B-F
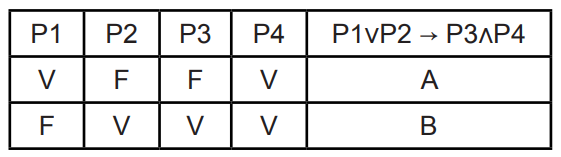
Resolução da operação de disjunção P1vP2
Apesar do enunciado do exercício ter detalhado tanto as proposições simples como compostas que compõe o problema a ser resolvido, para chegarmos a solução precisaremos apenas focar na tabela verdade cujos valores de cada proposição simples já se encontram devidamente preenchidos.
Para começarmos a resolução, devemos primeiramente resolver a operação lógica de disjunção P1vP2, conforme demonstrado abaixo:
| P1 | P2 | P1vP2 |
|---|---|---|
| V | F | V |
| F | V | V |
Resolução da operação de conjunção P3^P4
Em seguida vamos resolver a operação lógica de conjunção P3^P4, conforme demonstrado abaixo:
| P3 | P4 | P3^P4 |
|---|---|---|
| F | V | F |
| V | V | V |
- Resolução da operação condicional P1vP2→P3^P4
Por fim resolveremos a operação lógica condicional final entre os resultados encontrados nos passos anteriores da disjunção P1vP2 e da conjunção P3^P4, conforme demonstrado abaixo:
| P1vP2 | P3^P4 | P1vP2→P3^P4 |
|---|---|---|
| V | F | F |
| V | V | V |
Pela resolução demonstrada na tabela acima, a alternativa que lista corretamente os valores assumidos por A e B é a Letra B, ou seja, A assume o valor F e B assume o valor V.
Observação: A letra A assume o valor F de falso visto que proposições condicionais somente assumem o valor falso quando a primeira proposição for verdadeira e a segunda falsa.
A resolução de tabelas verdade deve seguir a ordem: proposições simples, negações, parênteses, conjunções, disjunções, condicionais e bi-condicionais.
No que segue, ~, ˅, ˄ e → representam os conectivos lógicos negação, disjunção, conjunção e condicional, respectivamente.
Qual das alternativas abaixo corresponde aos itens omissos da última coluna da tabela abaixo (de cima para baixo), onde V representa a Verdade e F a Falsidade?
A
V F V V V
B
V V F V V
C
V V V F V
D
V V V V F
E
F V V V V
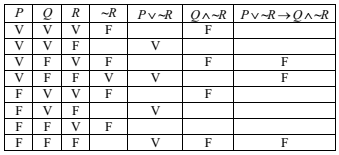
⚠️ Fique atento as informações preliminares.
Tabelas das principais operações de cálculo proposicional para resolução deste exercício.
- Negação (~)
A ~A V F F V - Conjunção (∧)
A B A ∧ B V V V V F F F V F F F F - Disjunção (v)
A B A v B V V V V F V F V V F F F - Condicional (->)
A B A -> B V V V V F F F V V F F V
✔️ Parabéns se você acertou. ❌ Se errou, saiba que nos tornamos melhores ao aprender com os erros.
Para começar, vamos resolver a negação da preposição R, ~R e preencher as lacunas vazias da tabela verdade dada no enunciado da questão.
| R | ~R |
|---|---|
| V | F |
| F | V |
| V | F |
| F | V |
| V | F |
| F | V |
| V | F |
| F | V |
Observação: Os valores lógicos em negrito e sublinhados em amarelo, indicam o preenchimento das lacunas vazias da tabela do enunciado do exercício.
Vamos resolver a disjunção(v) entre a preposição P e a negação ~R, e em seguida preencher as lacunas vazias da tabela verdade.
| P | ~R | Pv~R |
|---|---|---|
| V | F | V |
| V | V | V |
| V | F | V |
| V | V | V |
| F | F | F |
| F | V | V |
| F | F | F |
| F | V | V |
Observação: Os valores lógicos em negrito e sublinhados em amarelo, indicam o preenchimento das lacunas vazias da tabela do enunciado do exercício.
Vamos resolver a conjunção(∧) entre a preposição Q e a negação ~R, e preencher as lacunas vazias da tabela verdade antes da resolução da parte final do exercício.
| Q | ~R | Q∧~R |
|---|---|---|
| V | F | F |
| V | V | V |
| F | F | F |
| F | V | F |
| V | F | F |
| V | V | V |
| F | F | F |
| F | V | F |
Observação: Os valores lógicos em negrito e sublinhados em amarelo, indicam o preenchimento das lacunas vazias da tabela do enunciado do exercício.
Por fim, vamos resolver a condicional(->) entre Pv~R e Q∧~R que já foram previamente resolvidas, e preencher as lacunas vazias da última coluna da tabela verdade.
| Pv~R | Q∧~R | Pv~R->Q∧~R |
|---|---|---|
| V | F | F |
| V | V | V |
| V | F | F |
| V | F | F |
| F | F | V |
| V | V | V |
| F | F | V |
| V | F | F |
Observação: Os valores lógicos em negrito e sublinhados em amarelo, indicam o preenchimento das lacunas vazias da tabela do enunciado do exercício.
Após a resolução da última parte da tabela verdade, chegamos a alternativa correta Letra E - FVVVV, visto que o enunciado da questão nos pediu para marcar a opção que corresponde aos itens omissos da última coluna da tabela verdade, ou seja, os valores lógicos que preenchem por completo a última coluna da tabela verdade são FVFFVVVF e ao removermos os valores que foram previamente informados, ficamos com os valores FVVVV, que corresponde a resposta correta deste problema.
As proposições que compõe uma tabela verdade somente poderão ter valores falso ou verdadeiros pois segundo o princípio do terceiro excluído um enunciado ou é verdadeiro ou é falso, não existindo a possibilidade de um terceiro valor.
Considere as seguintes proposições:
A: O número 10 é ímpar; B: A raiz quadrada de 16 é um número inteiro.
Com base no exposto, assinale a alternativa correta.
A
A conjunção entre as duas proposições tem valor lógico verdade.
B
A disjunção entre as duas proposições tem valor lógico falso.
C
A condicional entre as duas proposições tem valor lógico verdade.
D
A bicondicional entre as duas proposições tem valor lógico verdade.
E
A negação de ambas as proposições tem valor lógico falso.
#Resumo
-
As alternativas "A", "B", "D" e "E" estão erradas e a alternativa "C" está correta, pois o valor lógico da proposição lógica A é falso pois 10 é um número par e o valor lógico da proposição B é verdadeiro visto que a raiz quadrada de 16 é o número inteiro 4. O que nos leva a única alternativa correta que diz que a condicional entre a proposição A e B tem o valor lógico de verdadeiro.
Veja também a resolução completa e detalhada.
De uma maneira geral, portas lógicas são definidas por tabelas verdade. A tabela verdade corresponde às saídas de um sistema para todas as combinações de entrada.
Para construir a tabela verdade da proposição ~ (pV ~q), um estudante montou o quadro apresentado.
Ao se preencher completamente e corretamente a tabela, o número de F encontrado na última coluna é igual a
A
1.
B
3.
C
4.
D
0.
E
2.
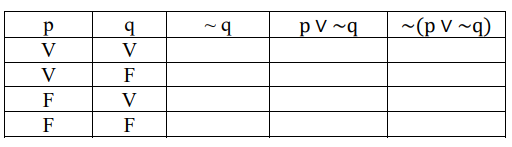
Preenchimento da coluna de negação (~q)
Primeiramente a negação da proposição ‘q’ será preenchida conforme a tabela parcial abaixo:
| p | q | ~q |
|---|---|---|
| V | V | F |
| V | F | V |
| F | V | F |
| F | F | V |
Preenchimento da coluna da disjunção (pv~q)
Anteriormente foi preenchido a coluna de negação ‘~q’, então o próximo passo para complementar a tabela verdade é a resolução da disjunção (pv~q).
| p | q | ~q | (pv~q) |
|---|---|---|---|
| V | V | F | V |
| V | F | V | V |
| F | V | F | F |
| F | F | V | V |
- Preenchimento da coluna de negação da disjunção ~(pv~q)
Por fim, para preencher completamente e corretamente a tabela verdade, basta resolver a negação da disjunção calculada na etapa anterior.
| p | q | ~q | (pv~q) | ~(pv~q) |
|---|---|---|---|---|
| V | V | F | V | F |
| V | F | V | V | F |
| F | V | F | F | V |
| F | F | V | V | F |
O número de F(falsos) encontrado na última coluna é igual a 3, conforme a resolução da tabela verdade acima, o que nos leva a resposta correta Letra B.
Tautologia ocorre quando uma dada proposição é sempre verdadeira, sem exceções. Uma tautologia significa que ao montarmos a tabela verdade, a última coluna sempre irá apresentar valores verdadeiros 'V'.
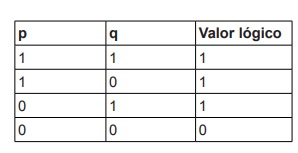
Analise a tabela a seguir, identifique qual operação lógica foi realizada e assinale a alternativa correta.
A
Disjunção.
B
Conjunção.
C
Negação.
D
Disrupção.
E
Equação.
- Parabéns!
A letra A está correta, pois na operação lógica de disjunção o resultado será verdadeiro quando pelo menos uma das proposições for verdadeira e o valor lógico será falso quando ambas as proposições forem falsas, conforme tabela verdade de disjunção abaixo:
| p | q | q v q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
- Errou?
A letra B está errada, pois na operação lógica de conjunção o resultado será verdadeiro somente quando todas as proposições forem verdadeiras e o resultado será falso quando existir uma proposição que seja falsa, conforme a tabela verdade abaixo:
| p | q | q ^ q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
A letra C está errada, pois na operação lógica de negação, basta inverter o valor lógico da proposição. Somente de olhar a primeira linha da tabela da ilustração do enunciado do exercício já sabemos que esta alternativa é incorreta, pois o valor lógico deveria ser 0 e não 1.
| p | q | ~p | ~q |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 |
A letra D e a letra E estão erradas, pois disrupção e equação não são operações lógicas. As únicas operações lógicas válidas são:
- Conjunção ( ˄ )
- Disjunção ( ˅ )
- Disjunção Exclusiva ( v )
- Condicional (→)
- Bicondicional (↔)
- Negação (~)
A contradição ocorre quando uma dada proposição é sempre falsa, ou seja, ao contrário do que ocorre na tautologia. Uma contradição significa que ao montarmos a tabela verdade, a última coluna sempre irá apresentar valores falsos 'F'.
Perguntas e Respostas
As convicções são inimigas mais perigosas da verdade do que as mentiras.