Espero que você aprenda muito com este exercício.
Aprofunde-se mais nos seus estudos com : Exercícios Resolvidos
10 exercícios resolvidos de matrizes para aprender sobre determinantes, inversas, sistemas lineares, operações e muito mais!
Resolva facilmente os exercícios de matrizes mais cobrados em provas e exames treinando e aprendendo gratuitamente com esta lista de exercícios resolvidos de matrizes.
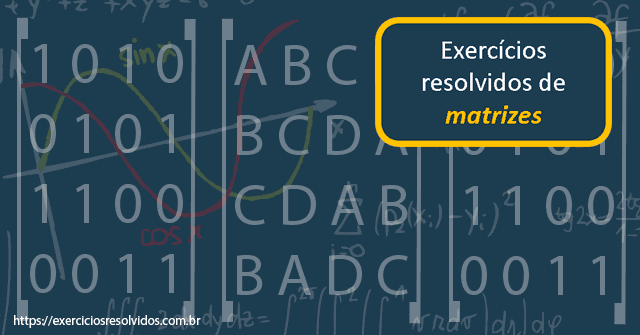
#Índice
Uma professora de matemática solicitou aos seus alunos que encontrassem o determinante da matriz abaixo. O valor encontrado foi:
A
3.112.
B
3.576.
C
4.006.
D
4.272.
E
Nenhuma das alternativas anteriores está correta.
Parte 1 da resolução
Determinante é uma função matricial que associa a cada matriz quadrada um escalar, ou seja, é uma função que transforma uma matriz quadrada em um número real.
| (M11) 54 | (M12) 120 |
| (M21) 13 | (M22) 108 |
Observação: A diagonal principal é composta pelos elementos M11 com valor 54 e M22 com valor 108, e a diagonal secundária é composta pelos elementos M21 com valor 13 e M12 com valor 120.
Para chegarmos a resposta Letra D 4.272 ,devemos subtrair a soma da diagonal principal da diagonal secundária, conforme demonstrado cálculo do determinante abaixo:
Um exemplo prático são os pixels da tela de um computador, tomando como exemplo uma tela com 640 x 480 pixels. Esses números indicam que a tela é formada por uma tabela com 307.200 pontos (área da tela), ou pixels. Essa tabela tem 480 pontos de altura e 640 pontos de largura. Para localizar um ponto nessa tabela, você pode dar como endereço um par (a,b), onde A seria a linha e B a coluna.
Considere uma matriz quadrada de ordem 3, cujos elementos aij sejam dados por aij = (i + j)^2. Pode-se afirmar que o determinante dessa matriz é um número:
A
Primo.
B
Negativo.
C
Ímpar.
D
Múltiplo de 3.
E
Múltiplo de 5.
Uma matriz transposta é uma matriz gerada através da troca ordenada das linhas pelas colunas. Se uma matriz é do tipo 3x2 (3 linhas e 2 colunas) a sua transposta será do tipo 2x3 (2 linhas e 3 colunas). Em computadores uma das circunstâncias mais comuns em que é necessário ou desejável reordenar fisicamente uma matriz na memória para sua ordem transposta, é para ganhar peformance de operações que localizam dados em memória.
Se a idade de Pedro é igual ao determinante da matriz A abaixo, é correto afirmar que Pedro possui:
A
50 anos.
B
56 anos.
C
58 anos.
D
63 anos.
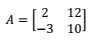
Parte 1 da resolução
Para calcularmos o determinante de uma matriz de ordem dois, devemos multiplicar os termos da diagonal principal e subtrair o resultado da multiplicação da diagonal secundária, o que nos leva a conclusão de que Pedro possui 56 anos, resposta Letra B, conforme demonstrado nos cálculos abaixo.
O Bloco Econômico MercoNorte é formado por 3 países do Hemisfério Norte. A matriz M a seguir mostra o volume de negócios realizados entre eles em 2016, na qual cada elemento aij a informa quanto o país i exportou para o país j, em bilhões de euros. No mesmo ano, o valor obtido com exportações pelo maior importador do Bloco foi de
A
5,7 bilhões de euros.
B
4,7 bilhões de euros.
C
4,5 bilhões de euros.
D
4,4 bilhões de euros.
Parte 1 da resolução
Este exercício é interessante por focar principalmente na interpretação de dados que uma matriz pode representar e também em como extrair informações relevantes a partir de uma matriz.
O enunciado da questão disse que "cada elemento aij a informa quanto o país i exportou para o país j", ou seja, as linhas indicam países que EXPORTAM e as colunas indicam o país que IMPORTAM. Perceba que a diagonal principal possui somente valores igual a zero pois um país não importa e nem exporta para ele mesmo.
Para simplificar a resolução do problema vamos supor que os nomes dos três países sejam Dinamarca, Finlândia e Suécia. Este nomes foram escolhidos levando em consideração que são países do hemisfério norte europeu e no enunciado do exercício foi dito que a moeda é o euro.
| Dinamarca | Finlândia | Suécia | |
| Dinamarca | (a11) 0 | (a12) 2,5 | (a13) 3,3 |
| Finlândia | (a21) 2,9 | (a22) 0 | (a23) 1,6 |
| Suécia | (a31) 1,5 | (a32) 3,2 | (a33) 0 |
Pela representação acima podemos extrair as seguintes informações com relação a cada país:
- Dinamarca
- Linhas
- Com relação ao elemento a11, a Dinamarca não importa e nem exporta nada para ela mesma.
- Com relação ao elemento a12, a Dinamarca EXPORTOU 2,5 bi para a Finlândia.
- Com relação ao elemento a13, a Dinamarca EXPORTOU 3,3 bi para a Suécia.
- Colunas
- Com relação ao elemento a21, a Dinamarca IMPORTOU 2,9 bi da Finlândia.
- Com relação ao elemento a31, a Dinamarca IMPORTOU 1,5 bi da Suécia.
- Balança comercial
- 5,8 - 4,4 = 1,4
- Finlândia
- Linhas
- Com relação ao elemento a21, a Finlândia EXPORTOU 2,9 bi para a Dinamarca.
- Com relação ao elemento a22, a Finlândia não importa e nem exporta nada para ela mesma.
- Com relação ao elemento a23, a Finlândia EXPORTOU 1,6 bi para a Suécia.
- Colunas
- Com relação ao elemento a12, a Finlândia importou 2,5 bi da Dinamarca.
- Com relação ao elemento a32, a Finlândia IMPORTOU 3,2 bi da Suécia.
- Balança comercial
- 4,5 - 5,7 = -1,2
- Suécia
- Linhas
- Com relação ao elemento a31, a Suécia EXPORTOU 1,5 bi para a Dinamarca.
- Com relação ao elemento a32, a Suécia EXPORTOU 3,2 bi para a Finlândia.
- Com relação ao elemento a33, a Suécia não importa e nem exporta nada para ela mesma.
- Colunas
- Com relação ao elemento a13, a Suécia IMPORTOU 3,3 bi da Dinamarca.
- Com relação ao elemento a23, a Suécia IMPORTOU 1,6 bi da Finlândia.
- Balança comercial
- 4,7 - 4,9 = -0,2
Observação: Saldo do balança comercial = Exportações - Importações
Pela análise da balança comercial de cada país sabemos que o maior importador do bloco foi a Finlândia, tendo importado 5,7 bi em 2016 e que ela exportou 4,5 bi, o que resultou em um déficit. Essa análise nos leva a resposta Letra C, já que os problema nos solicitou encontrar "o valor obtido com exportações pelo maior importador do Bloco".
O quadrado mágico é uma matriz quadrada de ordem n, cujos elementos são números inteiros 1, 2, ..., n², sem repetição, de tal modo que todas as linhas e todas as colunas têm a mesma soma (que se chama constante mágica). Considerando o disposto acima, é correto afirmar que a constante mágica de um quadrado mágico de ordem 15 é:
A
225
B
556
C
1695
D
3390
Suponha que, na Comissão de Farmácia Hospitalar do Conselho Federal de Farmácia, existam 5 computadores e 3 impressoras. Um sistema foi desenvolvido para controlar o número de páginas impressas diariamente. Esse sistema registra o número de páginas impressas em uma matriz na qual cada elemento ܽ registra o número de páginas enviadas pelo computador i para a impressora j. Ao final de determinado dia, verificou-se o registro da matriz, conforme apresentado na matriz abaixo.
Como exemplo, nesse dia, o computador 1 imprimiu 10 páginas na impressora 2. O total de páginas impressas pelos computadores 2, 3 e 5 na impressora 3 foi igual a
A
55.
B
62.
C
67.
D
72.
E
80.
Parte 1 da resolução
O enunciado dessa questão sobre matriz basicamente nos pede para somarmos a quantidade de páginas impressas pelos computadores 2, 3 e 5 na impressora 3.
Pela representação da matriz de computadores por impressoras sabemos que em um determinado dia o computador 2 imprimiu 25 páginas, o computador 3 imprimiu 7 páginas e o computador 5 imprimiu 30 páginas. A soma das páginas no leva a resposta letra B, 62 páginas impressas em um determinado dia na impressora 3 pelos computadores 2, 3 e 5.
- 25 páginas + 7 páginas + 30 páginas = 62 páginas
Observação: Perceba que este exercício se trata mais sobre interpretar os dados expostos em uma matriz do que necessariamente realizar algum tipo de cálculo mais complexo.
Considere a matriz A apresentada abaixo. Qual é o valor do determinante dessa matriz?
A
-36
B
-27
C
-15
D
+18
E
+45
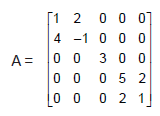
A matriz abaixo representa as quantidades de copos de sucos e vitaminas vendidas em uma lanchonete em um certo dia, nos períodos da manhã e da tarde. Se os preços cobrados por cada copo de suco e de vitamina são respectivamente R$ 3,00 e R$ 6,00 e o valor arrecadado de manhã e de tarde foram iguais, então o total de copos de sucos e vitaminas vendidos nesse dia foi igual a:
A
233.
B
265.
C
274.
D
277.
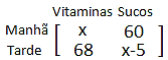
Marque a alternativa que apresenta os valores de x e y, respectivamente, para que as matrizes A e B sejam inversas.
A
1 e 3/10
B
3/10 e 2
C
3 e 4
D
1 e 2
E
- 1 e -3/10
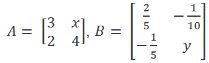
Parte 1 da resolução
Uma matriz inversa ou invertível é uma matriz quadrada que ocorre quando a multiplicação entre duas matrizes resultar em uma matriz identidade(elementos da diagonal principal são iguais a 1 e o restante são iguais a 0). Veja o exemplo de uma matriz identidade abaixo de ordem 2 x 2, que corresponde ao resultado da soma entre as matrizes A e B.
| 1 | 0 |
| 0 | 1 |
O exercício não deixou explícito qual operação será realizado, mas ao falar de matriz inversa logo sabemos que se trata de uma operação de multiplicação entre matrizes. O produto da multiplicação entre as matrizes se dá pela multiplicação/soma entre os elementos de linha da primeira matriz com os elementos de coluna da segunda matriz. Para melhor demonstração dos cálculos vamos chamar a matriz identidade de I, conforme demonstrado abaixo.
Para chegarmos à resposta Letra A x=1 e y=3/10 não foi preciso resolver as operações relativas a todos os elementos da matriz, somente foi calculado as funções com frações dos elementos de posição I11 e I22 para descobrirmos os valores das variáveis X e Y.
Marque a alternativa que apresenta os valores de x, y, z e w, respectivamente, para que a soma das matrizes A e B seja a matriz identidade
A
-1, -4, -7 e -4
B
6 e 0
C
4 e 5
D
3 e 7
E
0 e 6
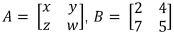
Parte 1 da resolução
Uma matriz identidade é uma matriz quadrada diagonal cujos elementos da diagonal principal são todos iguais a 1 e os demais elementos da matriz são iguais a 0. Veja o exemplo de uma matriz identidade abaixo de ordem 2 x 2, que corresponde ao resultado da soma entre as matrizes A e B.
| 1 | 0 |
| 0 | 1 |
O enunciado do exercício deixou bem claro que a operação de soma realizada entre a matriz A e B terá como resultado uma matriz identidade de ordem 2 x 2, ou seja, para chegarmos aos valores que representam x, y, z e w basta montarmos funções relativas as operações entre as matrizes. Para melhor demonstração dos cálculos vamos chamar a matriz identidade de I, conforme demonstrado abaixo.
Conforme demonstrado no cálculo da soma das matrizes abaixo, chegamos a resposta do exercício, Letra A x=-1, y=-4, z=-7 e w=-4
Observações:
A adição de matrizes deve ocorrer somente entre matrizes de mesma ordem sendo que o resultado da soma será uma outra matriz de mesma ordem, ou seja, se realizarmos a operação de adição entre duas matrizes de ordem 3 x 3 o resultado será uma nova matriz de ordem 3 x 3.
Os elementos somados entre uma matriz e outra devem ser correspondentes, ou seja, supondo uma matriz quadrada X, outra Y e outra de resultado R, todas de ordem 2, os elementos somados serão X11 + Y11 = R11, X12 + Y12 = R12, etc...
Perguntas e Respostas
Algumas pessoas acham que foco significa dizer sim para a coisa em que você irá se focar. Mas não é nada disso. Significa dizer não às centenas de outras boas idéias que existem. Você precisa selecionar cuidadosamente.