Espero que você aprenda muito com este exercício.
Aprofunde-se mais nos seus estudos com : Exercícios Resolvidos
10 exercícios resolvidos sobre regra de três composta para aprender sobre grandezas direta e inversamente proporcionais, razão e proporção e muito mais!
Solucione diversos exercícios de regra de três composta mais cobrados em provas, concursos e exames aproveitando para treinar e aprender gratuitamente com esta lista de exercícios.
#Índice
Três funcionários de uma oficina precisam de 10 minutos para transferir 24 pneus do depósito velho para o depósito novo. Vinte funcionários, todos com o mesmo rendimento de trabalho dos 3 iniciais, levaram 1 hora para transferir os pneus restantes do depósito velho para o depósito novo. O número de pneus que esses 20 funcionários transferiram foi
A
880
B
960
C
1040
D
1120
E
1200
Parte 1 da resolução
Nesta questão, identificamos que se trata de uma regra de três composta diretamente proporcional. Queremos descobrir o número de pneus que serão transferidos ao aumentar o número de funcionários, ou seja, uma grandeza diretamente proporcional acompanha o aumento da outra que será calculada.
Para se chegar a solução, o primeiro cálculo realizado é igualar as grandezas 10 minutos e 1 hora para a mesma unidade de medida, como demonstrado no cálculo abaixo que usa uma regra de três simples.
Apesar de se chegar a conclusão que 10 minutos equivalem à 0,16 horas, o raciocínio inverso facilitará o cálculo, ou seja, 1 hora é o mesmo que 60 minutos.
Parte 2 da resolução
Montar a tabela de relação entre as variáveis, conforme exemplo abaixo, não é necessário, mas ajuda a entender melhor o problema e resolver o problema rapidamente.
| Funcionários | Tempo (minutos) | Quantidade de pneus |
|---|---|---|
| 3 | 10 | 24 |
| 20 | 60 | X |
| ↑ | ↓ | ↑ |
Após a montagem da tabela a grandeza tempo diminui quando aumentamos a quantidade de funcionários, pois pela lógica 20 funcionários deveriam transferir 24 pneus em menos tempo que 3, ou seja, se o exercício pedisse para encontrar o valor da grandeza tempo, então seria uma regra de três inversamente proporcional.
Parte 3 da resolução
Por fim, o cálculo abaixo mostra a resolução das frações relativas a regra de três composta para se chegar a resposta Letra B 960 pneus transferidos por 20 funcionários.
A regra de três simples é usada em casos em que se identificam somente duas grandeza, enquanto que a regra de três composta é usada em casos que se identificam três grandezas.
Se 16 máquinas produzem 7.056 metros de tecido em 18 dias, então, supondo que cada uma das máquinas produz a mesma quantidade de tecido por dia, o número de máquinas necessário para produzir 10.829 metros de tecido em 17 dias é
A
25
B
24
C
27
D
26
E
28
Parte 1 da resolução
Pelo enunciado do exercício podemos perceber que se trata de uma regra de três composta inversamente proporcional, pois vamos descobrir a quantidade de máquinas necessárias para produzir mais tecido em menos tempo, 17 dias ao invés de 18 dias. Uma grandeza inversamente proporcional aumenta quando outra diminuí ou diminuí quando outra aumenta, ou seja, para produzir em menos dias deve-se aumentar a quantidade de máquinas, conforme a tabela montada abaixo:
| Máquinas | Quant. tecido produzido | Tempo |
|---|---|---|
| 16 | 7.056 metros | 18 dias |
| X | 10.829 metros | 17 dias |
| ↑ | ↑ | ↓ |
Parte 2 da resolução
Com a tabela de grandezas montada na parte 1 do exercício, basta resolver o cálculo das frações abaixa relativas a regra de três compostas para concluirmos que a resposta é a alternativa D 26 máquinas para produzir 10.829 metros de tecido em 17 dias.
Observação: Quando a regra de três é inversamente proporcional, para que o cálculo seja realizado deve-se inverter uma das razões.
Uma campanha de vacinação contou com 3 profissionais que conseguiram aplicar 600 vacinas em um período de 5 horas. Uma nova campanha contará com 8 profissionais, todos com a mesma eficiência daqueles da primeira campanha, que aplicarão 1280 vacinas. O número total de vacinas dessa nova campanha será aplicado em um período igual a
A
3h 20min.
B
4h.
C
4h 40min.
D
5h 20min.
E
6h.
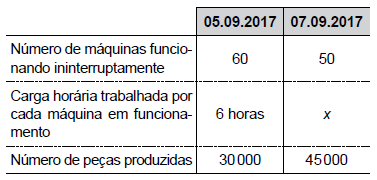
As informações apresentadas na tabela estão relacionadas à produção diária, totalmente automatizada, de uma determinada peça em uma grande indústria:
Considerando-se que todas as máquinas são iguais e têm a mesma produtividade, a carga horária trabalhada por cada máquina, no dia 07.09.2017 foi, exatamente,
A
10 horas e 48 minutos.
B
10 horas e 56 minutos.
C
11 horas e 04 minutos.
D
11 horas e 12 minutos.
E
11 horas e 20 minutos.
Para imprimir 300 apostilas destinadas a um curso, uma máquina de fotocópias precisa trabalhar 5 horas por dia durante 4 dias. Por motivos administrativos, será necessário imprimir 360 apostilas em apenas 3 dias. O número de horas diárias que essa máquina terá que trabalhar para realizar a tarefa é
A
25
B
24
C
27
D
26
E
28
Quatro máquinas idênticas produzem, em duas horas de trabalho, 2800 peças. Determine o tempo necessário, em horas, para que três dessas mesmas máquinas consigam produzir 21.000 peças.
A
20
B
18
C
15
D
12
E
10
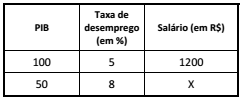
De acordo com a tabela abaixo, considerando que, quando a economia cresce, o desemprego cai e o salário aumenta, o valor de x será igual a:
A
960
B
600
C
375
D
305
E
120
Doze amigos planejam passar 5 dias em um acampamento e calcularam que deveriam levar, ao todo, 80 kg de alimento para serem consumidos uniformemente pelo grupo. Após receber mais dois integrantes, o grupo decidiu que ficariam 9 dias acampando. Considerando que todas as pessoas do grupo comerão a mesma quantidade de alimento por dia prevista, inicialmente, a quantidade de alimento, em kg, que será necessária é igual a:
A
156
B
160
C
164
D
168
E
172
Três máquinas iguais, trabalhando cinco horas por dia, durante sete dias produzem 231 kg de pregos. Para produzir 264 kg de pregos em apenas seis dias e com uma das máquinas parada, quantas horas por dia as máquinas precisarão trabalhar?
A
6h
B
7h
C
8h
D
10h
Para uma obra terminar em 10 dias, foram contratados 72 funcionários para trabalharem 8 horas por dia. Se a obra fosse para trinta dias, quantos funcionários deveriam ser dispensados, aproximadamente, para que a obra fosse concluída num regime de trabalho de 6 horas por dia?
A
56%
B
50%
C
43%
D
33%
E
27%
Perguntas e Respostas
Os problemas são oportunidades para se mostrar o que sabe.