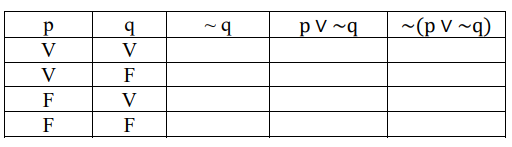
Para construir a tabela verdade da proposição ~ (pV ~q), um . . .
Exercício 9
Para construir a tabela verdade da proposição ~ (pV ~q), um estudante montou o quadro apresentado.
Ao se preencher completamente e corretamente a tabela, o número de F encontrado na última coluna é igual a
Resolução
Preenchimento da coluna de negação (~q)
Primeiramente a negação da proposição ‘q’ será preenchida conforme a tabela parcial abaixo:
| p | q | ~q |
|---|---|---|
| V | V | F |
| V | F | V |
| F | V | F |
| F | F | V |
Preenchimento da coluna da disjunção (pv~q)
Anteriormente foi preenchido a coluna de negação ‘~q’, então o próximo passo para complementar a tabela verdade é a resolução da disjunção (pv~q).
| p | q | ~q | (pv~q) |
|---|---|---|---|
| V | V | F | V |
| V | F | V | V |
| F | V | F | F |
| F | F | V | V |
- Preenchimento da coluna de negação da disjunção ~(pv~q)
Por fim, para preencher completamente e corretamente a tabela verdade, basta resolver a negação da disjunção calculada na etapa anterior.
| p | q | ~q | (pv~q) | ~(pv~q) |
|---|---|---|---|---|
| V | V | F | V | F |
| V | F | V | V | F |
| F | V | F | F | V |
| F | F | V | V | F |
O número de F(falsos) encontrado na última coluna é igual a 3, conforme a resolução da tabela verdade acima, o que nos leva a resposta correta Letra B.
Complementos
#Conceitos
Uma proposição lógica representa uma ideia completa que assume o valor lógico veradeiro ou falso.
A negação é uma operação lógica onde a proposição verdadeira se torna falsa, e proposição falsa se torna verdadeira, ou seja, basicamente é uma operação de inversão de valores lógicos.
A disjunção(ou) é uma operação lógica representada pelo conectivo 'v', intimamente ligada com a operação de união na teoria dos conjuntos, que resulta no valor lógico falso somente quando as demais proposições simples forem falsas.